Numerisk løsing av likninger (oppgave)#
Gå sammen i grupper på ca. fire personer og diskuter oppgavene nedenfor.
Oppgave 1#
a) Diskuter følgende spørsmål parvis i gruppa:
Hva er en likning?
Hva betyr det å løse en likning?
Hva er felles for alle nullpunkter?
b) Se på grafen til funksjonen f(x) nedenfor. Du kjenner ikke funksjonsuttrykket til denne grafen. Hvilke av følgende intervaller finnes nullpunktet i?
[-1, 0.5], [-1, 2], [0, 1], [0.5, 1], [1, 2], [-1, 2]
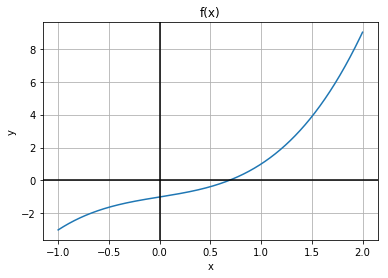
c) Hva er forskjellen mellom funksjonsverdien til funksjonen i randpunktene på de intervallene som inneholder nullpunktene og de som ikke gjør det? Er det noen systematisk sammenheng her?
d) Ta utgangspunkt i intervallet [0, 2]. Hvordan kan du justere dette intervallet systematisk for å komme nærmere og nærmere nullpunktet? Prøv å anvende generaliseringen om funksjonsverdiene ovenfor.
e) Prøv å formulere en enkel systematisk algoritme for å finne nullpunktet gitt et intervall.
f) Dere får utdelt noen grafer. En på gruppa får se grafene. Denne personen kan kun oppgi funksjonsverdier, mens de andre kan teste algoritmen dere lagde ovenfor ved å systematisk oppgi ulike x-verdier. Fungerte metoden på alle grafene?
Oppgave 2#
Vi har følgende funksjon:
a) Prøv å løse likninga \(f(x) = 0\) for hånd. Hvor langt kommer du med det? Dette kaller vi analytisk løsning av likninger, og vi ender opp med et eksakt svar hvis vi får det til.
b) Tegn grafen for funksjonen ovenfor og bruk metoden dere formulerte i oppgave 1 til å finne en tilnærma løsning. Dette kaller vi numerisk løsning av likninger.
