Polygontall

Du har kanskje hørt om kvadrattall? Og kanskje også trekanttall? Dette er tallfølger som hører innunder begrepet figurtall, nærmere bestemt polygontall. Et polygon kan også kalles mangekant eller n-kant. Polygontall er positive heltall som representerer et mønster ordnet i formen av en regulær polygon.

Figurtall lar oss visualisere tall som geometriske former. Å se ting på ulike måter får oss til å forstå verden på ulike måter, og kanskje lar det oss bidra med vårt eget, unike perspektiv. Det er essensen i matematikk.

Vi kan visualisere de seks første trekantallene slik:

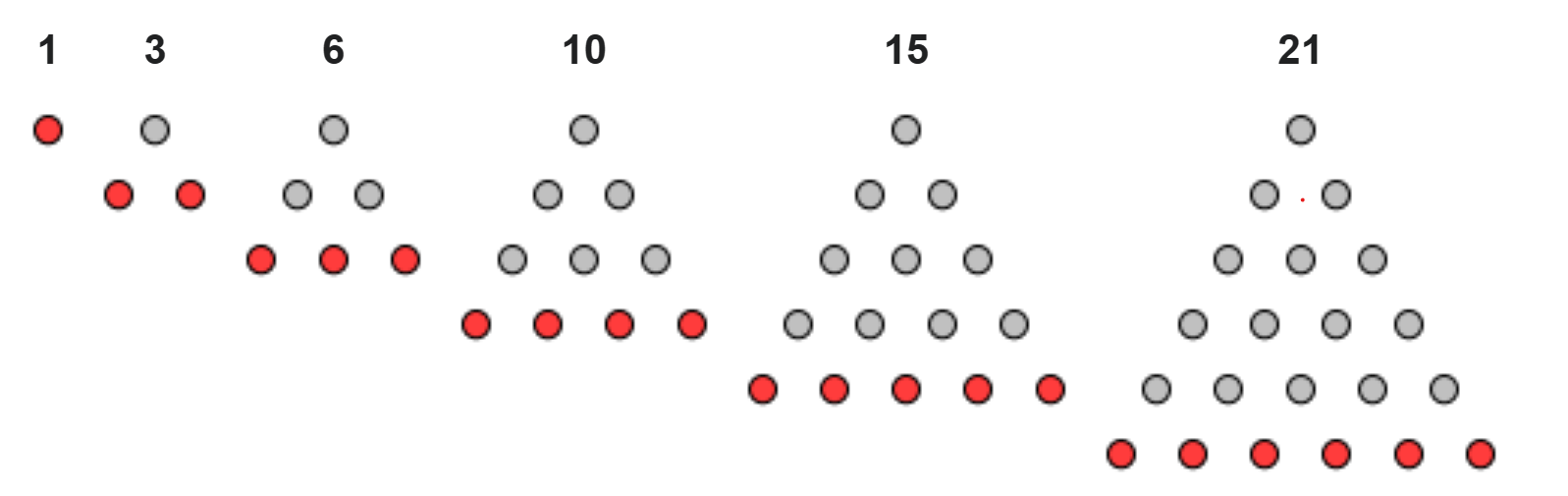
Du ser kanskje mønsteret?

Oppgave 1: Figur av firkanttall

Lag en figur som viser de fire første firkanttallene.

Vi kan representere firkanttallene med følgende formel, som beskriver hvordan et kvadrat med n sider inneholder \(K_n\) kuler:

\(K_{n+1} = K_n + (2n + 1)\)

Oppgave 2: Formel for trekanttall

Lag en formel som beskriver alle trekanttallene. Du kan starte med \(K_1 = 1\) for \(n = 0\). Bruk formelen til å finne trekanttall nr. 5.

Nå skal vi bruke programmering til å beskrive polygontallene. Først repeterer vi litt ved å bruke programmering til å beskrive et par enda enklere tallfølger: partall og oddetall.

Repetisjon: partall og oddetall

Partall er alle heltall som er delelige med 2, men vi kan også beskrive dem som en tallfølge der det neste tallet er det forrige + 2, og der vi starter med et tall, \(T_0\), som er delelig med 2:

\[T_{n+1} = T_n + 2\]

Tilsvarende blir det for oddetall, men da starter vi med et tall som ikke er delelig med 2. Vi tar utgangspunkt i denne måten å beskrive disse tallfølgene på i oppgavene nedenfor. Sørg for at du forstår notasjonen med indekser før du begynner (\(n + 1\) som indeks betyr “neste tall” og \(n\) betyr nåværende tall).

Oppgavene nedenfor skal dere gjøre sammen i par. Dere skal ha hver deres rolle, og bytte rolle for hver oppgave.

1. Rolle 1: Du skal forklare hva personen med rolle 2 skal skrive. Du skal ikke skrive kode selv.

2. Rolle 2: Du skal skrive koden som personen med rolle 1 forklarer. Du skal ikke komme med forslag til kode selv, med mindre personen med rolle 1 står fast en stund.

Oppgave 3: Partall

Nedenfor ser du et enkelt Python-program som skal regne ut alle partall fra 0 til og med 20. Fyll ut det som mangler for at programmet skal fungere.

Oppgave 4: Oddetall

Modifiser programmet i oppgave 3 slik at det skriver ut alle oddetall fra 1 til og med 21.

Oppgave 5: Partall med for-løkke

Modifiser programmet i oppgave 3 slik at det benytter en for-løkke istedenfor en while-løkke til å regne ut partallene.

Oppgave 6: Oddetall med for-løkke

Modifiser programmet i oppgave 4 slik at det benytter en for-løkke istedenfor en while-løkke til å regne ut oddetallene.

Polygontall

Nå kan vi bruke de samme strategiene som med partall og oddetall til å beskrive polygontall som trekanttall og firkanttall/kvadrattall. Løs oppgavene nedenfor. Det er valgfritt hvordan du løser dem, og om du løser dem alene eller sammen med en annen. Du skal presentere løsningene dine i en gruppe til slutt.

Oppgave 7: Trekanttall

Lag et program som finner trekanttall nr. 1000. Et nyttig tips her, er å starte med de 5 første trekanttallene og sjekke om programmet regner ut disse riktig. Deretter kan du utvide programmet slik at det finner trekanttall nr. 1000.

Oppgave 8: Firkanttall

Lag et program som skriver ut de 10 første firkanttallene.

Oppgave 9: Femkanttall

Lag et program som finner femkanttall nr. n.

Oppgave 10 (Utfordring): Fibonacci-tallene

Fibonnacifølgen er en kjent tallfølge med heltall der hvert tall etter det første er summen av de to foregående. Følgen starter slik: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, …

Lag et program som finner tall nr. n i rekka. Hvis du vil ha starthjelp, kan du klikke på hintet nedenfor - da får du litt kode som du kan starte med.

Hint: Fibonacci-tallene

Bruk dette uferdige programmet til å løse oppgava ovenfor. Trikset er å hele tida passe på hvilke verdier \(x_0\) og \(x_1\) har. Hvis vi overskriver en av verdiene med nye verdier, har vi ikke lenger tilgang til den gamle verdien. Dette kan vi løse ved å mellomlagre verdiene i andre variabler.

Sammensatte oppgaver

Fremgangsmåten du har brukt for å beskrive partall, odetall og polygontall, kan generaliseres og benyttes for alle tallfølger. Her skal du prøve deg på noen oppgaver der du kan bruke konseptene du utforsket ovenfor som utgangspunkt.

Oppgave 11: Bob-Kaares hurtigmat

Bob-Kaare er ferdig på videregående og har fått jobb i en hurtigmatkjede. Han har fått to tilbud fra sjegen sin. I tilbud 1 får han 100 kroner den første timen. Beløpet som han får den n-te timen er gitt ved:

\[a_n = a_{n-1} + 5\]

I tilbud 2 får han også 100 kroner den første timen. Beløpet som har får i den n-te timen er gitt ved:

\[b_n = b_{n-1}\cdot 1.03\]

a) Hvor mange timer tar det før tilbud 2 vil gi høyere timelønn enn tilbud 1?

b) Hvor mange timer tar det før tilbud 2 til sammen vil gi mer lønn enn tilbud 2?

Hint

Det kan være lurt å bruke en while-løkke til å løse oppgave 11. Da kan du bytte ut kriteriet for når den skal stoppe (f.eks. kan den gjenta til tilbud 2 er større enn tilbud 1).

Oppgave 12: På linje

I denne oppgava skal du arbeide med linjestykker som settes sammen til en figur. Skissen nedenfor viser de 16 første linjestykkene i figuren. Lengden av et linjestykke er alltid 90 % av lengden av det forrige linjestykket. Det første linjestykket er 100 cm langt.

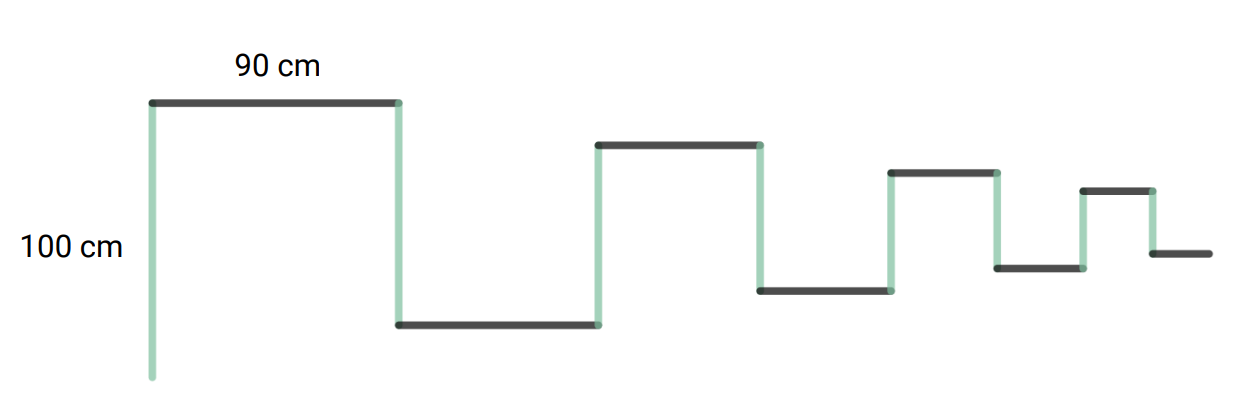
a) Bestem summen av lengdene av de 8 første linjestykkene i figuren.

b) Lag et program som du kan bruke til å bestemme summen av lengdene av linjestykkene dersom det er mange linjestykker i figuren. Hvor mange linjestykker må vi ha med i figuren dersom summen av lengdene skal bli minst 9 meter?

c) Hvor mange prosent øker summen av lengdene dersom vi øker antall linjestykker i figuren fra 50 til 100?