Matematiske algoritmer og stokastiske simuleringer#
Læringsutbytte
Etter å ha arbeidet med dette temaet, skal du kunne:
forklare noen matematiske algoritmer
programmere matematiske algoritmer
utføre og tolke stokastiske simuleringer
Algoritmer er presise, systematiske oppskrifter, og vi kjenner mange eksempler fra hverdagen. Eksempler er strikkeoppskrifter, kakeoppskrifter og algoritmene som gir oss anbefalte filmer på Netflix og annonser på Facebook. I matematikk er algoritmer framgangsmåter som lar oss løse et matematisk problem. Vi skal her se på noen gamle, klassiske matematiske algoritmer som har fått en renessanse med datamaskinen. Vi skal også se på hvordan vi bruker tilfeldige tall til å gjøre simuleringer. Først og fremst skal vi forstå hvordan algoritmene fungerer og hva de kan brukes til. Vi skal også prøve å programmere noen av algoritmene.
Primtall med Eratosthenes sil#
La oss først se på en gammel metode som kan brukes til å finne primtall. Eratosthenes sil er en metode som ble utviklet av den greske matematikeren Eratosthenes i ca. 200 f. Kr. Metoden er enkel og systematisk, og er derfor også programmerbar. Metoden fungerer slik:
Lag ei liste av påfølgende heltall fra 2 til 100 med ti tall på hver rad (bortsett fra den første). Se tabellen nedenfor.
La p til å begynne med være lik 2, det første primtallet.
Stryk ut alle multipler av p som er større enn eller lik \(p^2\).
Finn det første tallet større enn p som står igjen på lista. Dette tallet er det neste primtallet. Sett p lik dette tallet.
Gjenta trinn 3 og 4 inntil \(p^2\) er større enn 100.
Alle gjenværende tall på listen er primtall!
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
21 |
22 |
23 |
24 |
25 |
26 |
27 |
28 |
29 |
30 |
31 |
32 |
33 |
34 |
35 |
36 |
37 |
38 |
39 |
40 |
41 |
42 |
43 |
44 |
45 |
46 |
47 |
48 |
49 |
50 |
51 |
52 |
53 |
54 |
55 |
56 |
57 |
58 |
59 |
60 |
61 |
62 |
63 |
64 |
65 |
66 |
67 |
68 |
69 |
70 |
71 |
72 |
73 |
74 |
75 |
76 |
77 |
78 |
79 |
80 |
81 |
82 |
83 |
84 |
85 |
86 |
87 |
88 |
89 |
90 |
91 |
92 |
93 |
94 |
95 |
96 |
97 |
98 |
99 |
100 |
Underveisoppgave
Utfør algoritmen for hånd. Å programmere algoritmen er litt ufordrendende, men du kan prøve på det når du er ferdig med å gjøre algoritmen for hånd.
Slik kan du programmere algoritmen
Her lager vi en funksjon, men du kan godt gjøre det uten funksjoner.
from pylab import *
def eratosthenes_sil(n):
tall = list(arange(2,n+1,1)) # Lager array med heltall fra 2 til og med n
i = 0
# Algoritmen begynner
p = tall[i]
while p**2 <= n:
for element in tall:
if element%p == 0 and element >= p**2:
tall.remove(element)
i = i + 1
p = tall[i]
return tall
primtall = eratosthenes_sil(100)
print(primtall)
Kvadratrøtter med gammel babylonsk algoritme#
En annen gammel algoritme kommer fra Babylonia, og er godt over 2000 år gammel. Den ble brukt til å finne kvadratrota av et tall. Du kan se utledning av algoritmen i videoen nedenfor:
Algoritmen fungerer slik:
Gjør en kvalifisert gjetning på hva \(\sqrt{a}\) er, og kall gjetningen \(x_0\). Gjenta følgende algoritme \(n\) ganger:
\(x_{n+1} = \frac{1}{2}\left(x_n+\frac{a}{x_n}\right)\)
Underveisoppgave
Test algoritmen på \(\sqrt{12} \approx 3.46410161514\). Regn ut feilen for hver iterasjon (gjentakelse i løkka). Eksperimenter med algoritmen på andre tall.
Stokastiske simuleringer: Monte-Carlo-metoder#
En stokastisk simulering er en simulering der tilfeldige hendelser inntreffer med en viss sannsynlighet. Det er mange prosesser i naturen som er tilfeldige eller delvis tilfeldige, f.eks. radioaktivt henfall, mutasjoner og diffusjon. Slike simuleringer er oppkalt etter kasinoet i Monte Carlo, og kalles Monte Carlo-metoder, fordi de benytter tilfeldige tall som grunnlag for det de skal tilnærme. Det er enormt mange anvendelser av MC-metoder. Vi skal se på noen av dem her. Men først skal vi ta en kikk på hvordan vi kan bruke simuleringer til å illustrere hva sannsynlighet er. Da trenger vi å kunne generere tilfeldige tall på datamaskinen. Dette kan vi gjøre slik:
import numpy as np
heltall = np.random.randint(1, 10) # lager et tilfeldig heltall i intervallet [1, 9]
flyttall = np.random.uniform(-1, 1) # Lager et tilfeldig flyttall mellom -1 og 1
Underveisoppgave
Lag en funksjon som tar som parameter antallet ganger n du skal kaste en terning. Funksjonen skal returnere ei liste med n terningkast.
Løsningsforslag
import numpy as np
def terningkast(n):
resultater = []
for i in range(n):
kast = np.random.randint(1,7)
resultater.append(kast)
return resultater
print(terningkast(6))
Sannsynlighetsbegrepet#
Vi bruker sannsynlighet til vurderinger av hva vi skal gjøre i hverdagen hele tida. Er det trygt å gå over gata? Bør jeg spille Lotto? Er det lurt å klatre opp denne bratte, glatte fjellskrenten? Men hva er sannsynlighet egentlig? La oss prøve å bruke programmering for å finne ut av dette.
Vi skal studere et program som simulerer myntkast. Klikk på de ulike fanene for å gjøre oppgava tilpasset din kompetanse i programmering. Dersom du for eksempel forstår programmering godt, kan du prøve å lage programmet helt fra scratch. Da klikker du deg inn på nivå 5. Du kan starte på det nivået som passer deg. Prøv også gjerne de andre nivåene etter hvert. Det kan være mye lærering i å gå nedover i nivå også!
Nivå 1: Forklar og modifiser
Nivå 2: Programmeringspuslespill
Nivå 3: Feilsøk
Nivå 4: Fyll inn
Nivå 5: Lag programmet
Forklar hva programmet nedenfor gjør før du kjører programmet.
Kjør deretter programmet og forklar hva det kan fortelle deg om sannsynlighet.
Modifiser programmet slik at det kaster mynten 100 ganger, 1000 ganger og 10000 ganger. Hva blir utfallet, og hvorfor?
Løs dette puslespillet. Programmet skal simulere et myntkast og finne relativ frekvens av antall mynt, dersom kron = 0 og mynt = 1.
Programmetet nedenfor skal simulere et myntkast og finne relativ frekvens av antall mynt, med kron = 0 og mynt = 1, men programmet fungerer ikke som det skal. Forklar hva som er feil, og hvorfor. Rett opp programmet slik at det fungerer. Kjør programmet flere ganger med ulikt antall kast. Hva forteller resultatene deg om sammenhengen mellom relativ frekvens og sannsynlighet?
Programmet nedenfor skal simulere et myntkast og finne relativ frekvens av antall mynt, med kron = 0 og mynt = 1. Fyll inn det som mangler. Kjør deretter programmet flere ganger med ulikt antall kast. Forklar hva programmet kan fortelle deg om sammenhengen mellom relativ frekvens og sannsynlighet.
Lag et program som skal simulere et myntkast og finne relativ frekvens av antall mynt. Varier antallet kast. Hva forteller resultatene deg om sammenhengen mellom relativ frekvens og sannsynlighet?
Tilnærming av pi med Monte Carlo-metoder#
Selv om \(\pi\) er et bestemt tall, kan vi faktisk tilnærme \(\pi\) med tilfeldige tall. En Monte Carlo-algoritme for å estimere pi baserer seg på følgende:
\(A=\pi r^2\), så hvis \(r = 1\), er \(A = \pi\).
Lag et kvadrat med sidelengder = 2 og en innskrevet sirkel med radius = 1:
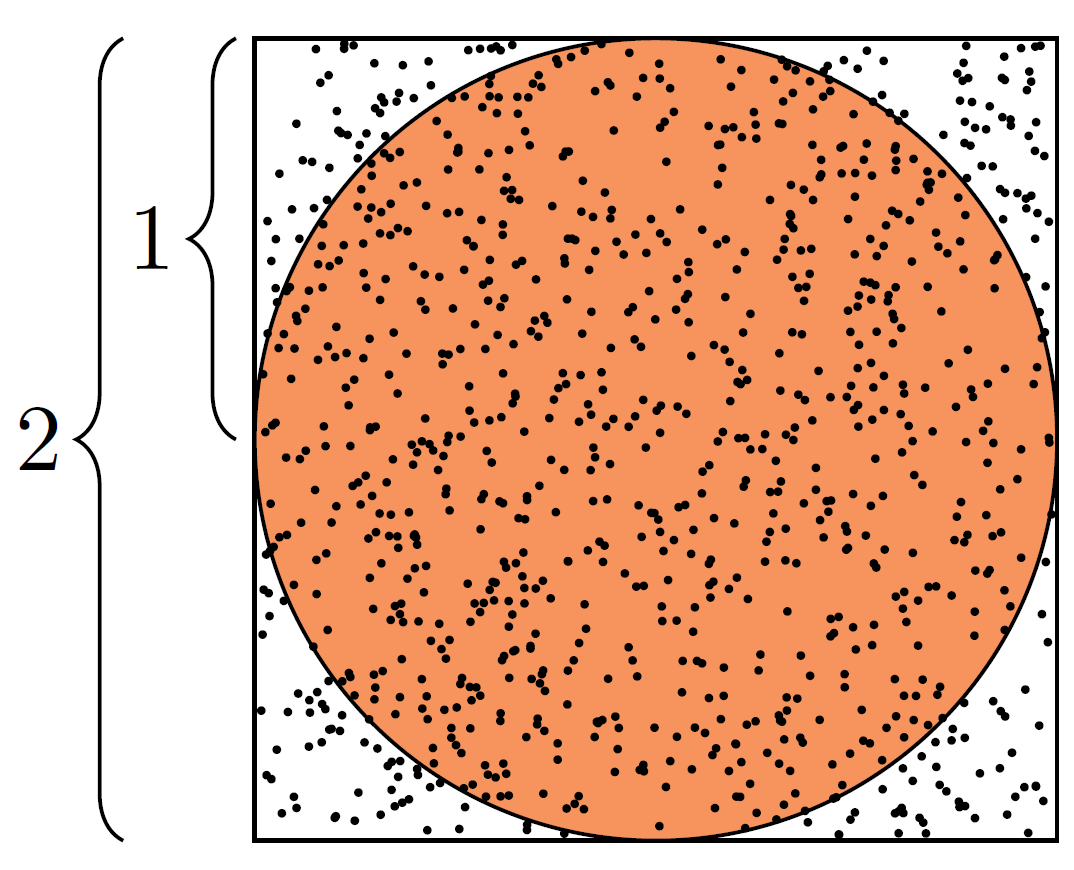
Trekk N tilfeldige tall av et x-koordinat og et y-koordinat.
Sjekk om \((x, y)\) ligger inni eller på sirkelen (\(x^2+y^2\leq 1\)).
Sett M lik antall punkter som treffer sirkelen.
Nå er \(\pi = A_{sirkel} = A_{kvadrat} \cdot \frac{M}{N}\)
Beregn \(\pi\) og regn avviket fra den «eksakte» verdien.
Brownske bevegelser (enkel diffusjon)#
Vi skal her se på en MC-tilnærming til tilfeldig bevegelse av store partikler i løsning. Dette er en enkel modell for diffusjon av ikke-reagererende partikler som kan beskrive såkalte Brownske bevegelser. Brownske bevegelser ble først beskrevet av botanisten Robert Brown i 1827. Han oppdaga at små pollenkorn i løsning beveget seg fram og tilbake i et tilfeldig mønster. I dag veit vi at dette skyldes at de små vannmolekylene dytter på pollenkornet i mange tilfeldige retninger. Det samme gjelder større partikler som enkelte luktmolekyler (parfyme) og røyk, som vi jo kan lukte og noen ganger observere direkte i makroskala.

For å simulere det som skjer på mikroskala, kan vi lage et program der vi for hvert tidssteg trekker tilfeldige tall som bestemmer retningen til partikkelen. Vi kan først se på hvordan vi kan gjøre dette ved å konstruere et rutenett der en partikkel kan bevege seg i fire retninger (opp, ned, høyre og venstre). Skråbevegelser kan beskrives som en kombinasjon av disse bevegelsene:
Disse bevegelsene kan vi representere med posisjonsarrayer \(x\) og \(y\). Posisjonen kan starte i origo, \((0, 0)\), og så kan vi øke eller redusere med 1 i en tilfeldig retning. Dette kan vi gjøre ved å trekke et tilfeldig tall mellom 1 og 4 som representerer bevegelse i rutenettet slik:
Hvis vi for eksempel trekker tallet 4, vil partikkelen bevege seg én rute nedover i \(y\)-retning. Da trekker vi fra 1 i arrayen som inneholder \(y\)-koordinatene.
Underveisoppgave
Bruk programmet nedenfor som utgangspunkt for å simulere bevegelsen til partikkelen:
Underveisoppgave
Bruk skilpaddegrafikk (turtle) til å simulere bevegelsen til partikkelen. Du skal lage en skilpadde som beveger seg i en tilfeldig retning (tilfeldig vinkel) en bestemt avstand (for eksempel 5) for hvert tidssteg.
Oppgaver#
Oppgave 1
Utled og forklar den gamle babylonske algoritmen for å finne kvadratrøtter.
Oppgave 2
Lag spillet Yatzy.
Oppgave 3
Bruk simuleringer til å regne ut hva sannsynligheten for at det i vår klasse er minst 2 personer som har samme bursdag. Hvilke forutsetninger må ta gjøre for å utføre simuleringen?
Oppgave 4
I koden nedenfor har vi gjort et forsøk på å sette opp terminlisten for Eliteserien 2024, men koden er uferdig og virker enda ikke som den skal. Kjør koden, så ser du at vi ikke lykkes med å la alle lagene møte hverandre 2 ganger. Men legg merke til at det alltid er første lag i hjemmelag-listen som møter første lag i bortelag-listen, og ditto for andre lag i hver liste, tredje lag osv.
a) For at det ikke skal bli de samme kampene i hver eneste runde, må vi flytte lagene rundt i listene. En måte å gjøre det på er at vi fjerner det siste laget i hjemmelag-listen og legger det sist i bortelag-listen, samtidig som vi flytter det første laget i bortelag-listen først i hjemmelag-listen. Da får vi en rotasjon som gjør listene endrer seg på denne måten:
# Før første rotasjon
["Bodø/Glimt", "Brann", "Fredrikstad", "HamKam", "Haugesund", "KFUM Oslo", "Kristiansund", "Lillestrøm"]
["Molde", "Odd", "Rosenborg", "Sandefjord", "Sarpsborg 08", "Strømsgodset", "Tromsø", "Viking"]
# Etter første rotasjon
["Molde", "Bodø/Glimt", "Brann", "Fredrikstad", "HamKam", "Haugesund", "KFUM Oslo", "Kristiansund"]
["Odd", "Rosenborg", "Sandefjord", "Sarpsborg 08", "Strømsgodset", "Tromsø", "Viking", "Lillestrøm"]
# Etter andre rotasjon
["Odd", "Molde", "Bodø/Glimt", "Brann", "Fredrikstad", "HamKam", "Haugesund", "KFUM Oslo"]
["Rosenborg", "Sandefjord", "Sarpsborg 08", "Strømsgodset", "Tromsø", "Viking", "Lillestrøm", "Kristiansund"]
Ser du at lagene går rundt og rundt hvis vi fortsetter å rotere på denne måten? Legg
Nå som vi vet hva vi skal gjøre, må vi se på hvordan. Du kan bruke disse metodene på lister (før du går løs på de store listene, kjør gjerne denne testkoden selv og skriv ut listene for å se hva som skjer):
en_liste = [1, 2, 3]
siste_element = en_liste.pop() # fjerner siste element fra listen (og lagrer det i en variabel så vi ikke mister dette elementet)
# en_liste har nå verdien [1, 2]
en_liste.insert(0, siste_element) # setter inn verdien til variabelen på indeks 0, først i listen
# en_liste har nå verdien [3, 1, 2]
første_element = en_liste.pop(0) # fjerner første element (indeks 0) fra listen (og lagrer det i en variabel)
# en_liste har nå verdien [1, 2]
en_liste.append(første_element) # setter inn verdien til variabelen helt sist i listen
# en_liste har nå verdien [1, 2, 3]
Bruk disse metodene til å gjøre rotasjonen over på riktig sted (merket med TODO) i Trinket-koden. Kjør koden og se hva som skjer. Fungerer rotasjonen som i eksempelet over?
b) Som du la merke til, møtes de fleste lagene 2 ganger, som er det vi ønsker, men ikke alle! Løsningen på det er å la ett lag være statisk (i ro) mens de andre roterer rundt, for eksempel slik:
# Før første rotasjon
["Bodø/Glimt", "Brann", "Fredrikstad", "HamKam", "Haugesund", "KFUM Oslo", "Kristiansund", "Lillestrøm"]
["Molde", "Odd", "Rosenborg", "Sandefjord", "Sarpsborg 08", "Strømsgodset", "Tromsø", "Viking"]
# Etter første rotasjon
["Bodø/Glimt", "Molde", "Brann", "Fredrikstad", "HamKam", "Haugesund", "KFUM Oslo", "Kristiansund"]
["Odd", "Rosenborg", "Sandefjord", "Sarpsborg 08", "Strømsgodset", "Tromsø", "Viking", "Lillestrøm"]
# Etter andre rotasjon
["Bodø/Glimt", "Odd", "Molde", "Brann", "Fredrikstad", "HamKam", "Haugesund", "KFUM Oslo"]
["Rosenborg", "Sandefjord", "Sarpsborg 08", "Strømsgodset", "Tromsø", "Viking", "Lillestrøm", "Kristiansund"]
Ser du hvilket lag som nå står i ro? Hva må du endre i insert-metoden for å få dette til? Eksperimenter og sjekk at endringen gjør at alle lagene møter hverandre 2 ganger.
Algoritmen du nå har programmet kalles round-robin-algoritmen og er en klassisk algoritme for å sette opp en serie hvor alle møter alle.
c) For at det skal bli mest mulig rettferdig, bør lagene ha en hjemmekamp og en bortekamp mot hverandre. For å få til det, kan vi la laget fra bortelag-listen være hjemmelag hvis det er en partallsrunde, altså hvis r + 1 er delelig på 2.
x = 4
if x % 2 == 0:
print("Tallet er delelig på 2")
else:
print("Tallet er ikke delelig på 2")
Endre koden slik at alle lagene får en hjemmekamp og en bortekamp mot hverandre (alle kampene blir da unike og spilles bare 1 gang).
Fungerer dette også dersom vi fjerner Lillestrøm og Viking, og dermed reduserer antall lag fra 16 til 14? Prøv å endre koden til å teste dette. Hvorfor fungerer det / fungerer det ikke?
Oppgave 5 (utfordring)
Det er 100 plasser i et fullbooket fly, men fordi du kommer for seint, er du den siste personen i køen som kommer inn. Den første i køen er litt idiot, og velger derfor en tilfeldig plass på flyet. Så kommer 98 Hell’s Angels (én etter én). Disse bikergjengmedlemmene er ganske tydelige, og så fort de ser noen på plassen deres, grynter de, og idioten (som sitter i setet deres) må flytte seg (tilfeldig) til et annet sted. Til slutt, når alle er inne, så kommer du.
Hva er sannsynligheten for at noen sitter i setet ditt?
Hvor mange ganger i snitt bytter den første personen sete?
