Løsing av likninger (1T)#
Relevante kompetansemål
formulere og løse problemer ved hjelp av algoritmisk tenkning, ulike problemløsingsstrategier, digitale verktøy og programmering
utforske strategier for å løse ligninger, ligningssystemer og ulikheter og argumentere for tenkemåtene sine
Løsing av likninger#
Her skal vi se på en oppgave der vi jobber med ulike strategier for å løse likninger. Oppgava er utformet etter PRIMM-prinsippet. PRIMM står for Predict-Run-Investigate-Modify-Make, og er en metode som kan brukes til å bygge opp programmeringsoppgaver på en gradvis måte. I tillegg vil en gjennom PRIMM-oppgaver kunne ha større fokus på det faglige innholdet.
Oppgave (PRIMM)
I denne oppgava skal vi løse likningen \(e^{-x} + x + 5 - \log(0.006x + 1) - x^{0.3} - 10 = 0\). Denne likningen er ikke analytisk løsbar, så vi må bruke numeriske metoder for å løse den.
a. Se på programmet nedenfor uten å kjøre det. Hva gjør programmet? Tegn gjerne en figur som hjelper deg å forstå hva programmet gjør. Du kan klikke på ruta nedenfor for å få et hint til hva som skjer. Her brukes det en enklere funksjon, men poenget er det samme.
Hint: Figur

b. Test programmet og se hva det gjør. Tegn grafen i Python og verifiser at programmet gjør det det skal.
c. Prøv å løse likningen \(x^2 - 4 = 0\) med metoden ovenfor. Fant du alle løsningene? Plott gjerne grafen til funksjonen \(f(x) = x^2 - 4\) og sammenlikn med nullpunktene du ser. Diskuter det du finner ut med en annen som har gjort oppgaven.
d. Modifiser programmet slik at det istedenfor å bruke funksjoner, benytter funksjonsverdier som er forhåndslagret i en array eller liste. Du kan lage arrayene og starten av løkka slik:
Test om programmet gir samme nullpunkt som før. Prøv også nå å løse likningen \(x^2 - 4 = 0\) ved å lage et x-intervall fra -10 til 10, og sammenlikn med resultatet fra den forrige metoden. Hva er forskjellen, og hvorfor fikk du denne forskjellen?
e. En annen metode for å løse likninger kalles halveringsmetoden. Bruk det første programmet du lagde som inspirasjon til å lage et program som bruker denne metoden. Halveringsmetoden går ut på å velge et intervall \([a, b]\) der \(f(a)\) og \(f(b)\) har motsatte fortegn. Vi kan bruke grafen til å vurdere hvilket intervall som egner seg dersom vi plotter den først. Deretter skal vi finne et nytt intervall \([a, b]\) som er mindre, men slik at \(f(a)\) og \(f(b)\) fortsatt har motsatte fortegn. Det kan vi gjøre ved å finne midten mellom a og b. Da får vi et punkt \(m = (a + b)/2\), og vi kan finne \(f(m)\).
Vi undersøker så om \(f(m_1) = 0\). Hvis ikke, evaluerer vi fortegnene til \(f(a)\), \(f(b)\) og \(f(m)\). Dersom \(f(a)\) og \(f(m)\) har samme fortegn, setter vi det nye intervallet til \([m, b]\) fordi da må \(f(m)\) og \(f(b)\) ha motsatte fortegn. Motsatt setter vi intervallet til \([a, m]\) dersom \(f(b)\) og \(f(m)\) har samme fortegn. Prosessen gjentas n ganger til vi har at \(f(m_n) \approx 0\). Figuren nedenfor illustrerer metoden med to trinn
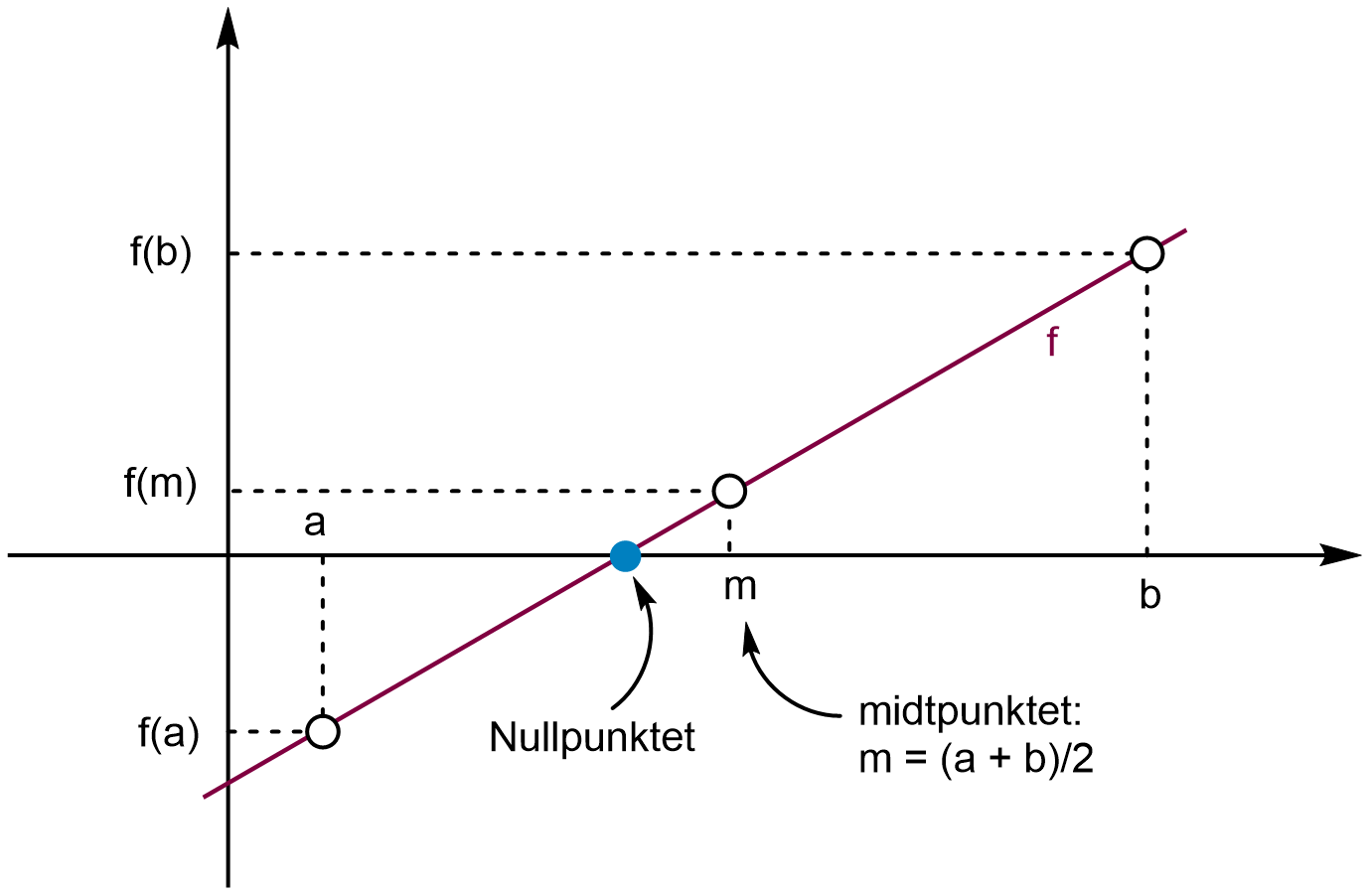
Algoritmen kan mer generelt beskrives slik:
Halveringsmetoden
La f være en kontinuerlig funksjon med motsatte fortegn på funksjonsverdiene \(f(a)\) og \(f(b)\) i intervallet \([a,b]\). Da kan nullpunktene finnes slik:
Finn midtpunktet \(c_k\) mellom punktene a og b.
Undersøk hvilke av \(f(a)\) og \(f(b)\) som har motsatt fortegn til \(f(c_k)\), og sett det nye intervallet til \([a,c_k]\) eller \([c_k, b]\), der start- og sluttverdien i intervallet skal ha motsatt fortegn.
Gjenta prosessen n ganger til \(f(c_k) \approx 0\).
Programmet nedenfor gir deg litt starthjelp.
Du kan også klikke på hintet nedenfor for å se en pseudokode som beskriver algoritmen:
Definer funksjon f(x)
a = -10
b = 10
m = (a+b)/2
Gjenta så lenge f(m) ikke er lik null:
hvis f(a)*f(m) er mindre enn 0:
b = m
hvis f(b)*f(m) er mindre enn 0:
a = m
m = (a+b)/2
Skriv ut m
