Statistikk

Læringsutbytte

Etter å ha arbeidet med dette temaet, skal du kunne:

1. bruke deskriptiv statistikk til å beskrive data med tall og visualiseringer

2. utføre regresjonsanalyse og tolke resultatene

If your experiment needs a statistician, you need a better experiment.

—Fysikeren Ernest Rutherford (1871–1937)

Deskriptiv statistikk

Vi kan bruke statistikk til å oppsummere, beskrive og tolke data. Vi skiller mellom to typer statistikk:

1. Deskriptiv statistikk: oppsummere og beskrive data

2. Statistisk interferens: trekke slutninger fra data

Vi skal mest se på deskriptiv statistikk her. La oss vende tilbake til pingvindataene våre. Vi kan få en enkel statistisk oversikt over datasettet vårt ved å bruke funksjonen describe.

import pandas as pd

pingvindata = pd.read_csv("data/penguins.txt", delimiter = ",")
pingvindata.describe()

	bill_length_mm	bill_depth_mm	flipper_length_mm	body_mass_g
count	342.000000	342.000000	342.000000	342.000000
mean	43.921930	17.151170	200.915205	4201.754386
std	5.459584	1.974793	14.061714	801.954536
min	32.100000	13.100000	172.000000	2700.000000
25%	39.225000	15.600000	190.000000	3550.000000
50%	44.450000	17.300000	197.000000	4050.000000
75%	48.500000	18.700000	213.000000	4750.000000
max	59.600000	21.500000	231.000000	6300.000000

Vi kan forklare disse størrelsene slik:

• count = antall registrerte tilfeller

• mean = gjennomsnittet for alle individer

• std = standardavviket (dette skal vi se nærmere på seinere)

• min = minste registrerte verdi

• 25 % = “nedre kvartil”. Her har 25 % av pingvinene for eksempel en kroppsmasse mellom 3550 og minste verdi (2700).

• 50 % = “midtre kvartil”. Her har 50 % av pingvinene for eksempel en kroppsmasse mellom 3550 og 4050.

• 75 % = “øvre kvartil”. Her har 75 % av pingvinene for eksempel en kroppsmasse på 4750 eller under. Det betyr også at 25 % har en kroppsmasse på 4750 til maksverdien 6300.

• max = høyeste registrerte verdi

Vi kan også finne mange av disse størrelsene ved å bruke ulike funksjoner:

Underveisoppgave

Prøv ut programmet ovenfor og utforsk de ulike variablene slik at du forstår hva alle de statistiske størrelsene betyr. Forklar begrepet kvartil.

Mål på spredning

Det finnes mange måter å beskrive spredningen i en variabel på. Vi skal se på følgende måter:

• Variasjonsbredde

• Interkvartilbredde

• Varians og standardavvik

Variasjonsbredde er et enkelt mål på spredning, nemlig differansen mellom største og minste verdi (\(x_{maks} - x_{min}\). De to andre målene må vi se litt nøyere på.

Underveisoppgave

Regn ut variasjonsbredden i nebbdybde hos pingvinene.

Interkvartilbredde

Vi har sett hvordan vi kan regne ut kvartiler.

Kvartiler og persentiler

Kvartiler er fjerdedeler av et utvalg. For eksempel er nedre kvartil (\(Q_1\)) den høyeste verdien av en variabel som tilhører de 25 % minste verdiene innenfor en variabel. Midtre kvartil (\(Q_2\)) er verdien midt i datasettet, det vil si at 50 % av dataene ligger over og under dette punktet. Den midtre kvartilen kalles også for medianen. Tredje kvartil (\(Q_3\)) markerer verdien som 75 % av dataene ligger under (og de resterende 25 % av dataene ligger over).

Dersom vi bruker en vilkårlig prosent som ikke representerer en fjerdedel, kaller vi det en persentil.

Differansen mellom første og tredje kvartil er et godt mål på spredning. Dette er et mål på spredningen til de 50 % midtre dataene, og påvirkes derfor ikke av data som ligger langt unna de andre dataene (såkalte “uteliggere”). Dette målet kalles interkvartilbredde (IQR) eller bare kvartilbredde:

\(IQR = Q_3 - Q_1\)

Kvartiler kan visualiseres enkelt med et boksplott:

import seaborn as sns

sns.boxplot(data = pingvindata, x = "species", y = "bill_depth_mm")

<AxesSubplot:xlabel='species', ylabel='bill_depth_mm'>

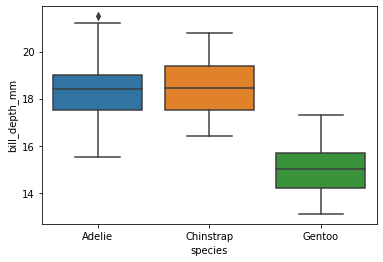
Vi kan forklare dette plottet slik:

• Den svarte linja midt i boksene er medianen.

• 50 % av verdiene ligger innenfor boksene. Boksene markerer altså interkvartilområdet, fra \(Q_1\) til \(Q_3\).

• Vi har to utstikkere på hver side av boksen. De viser \(IQR\cdot1.5 = 1.5(Q_3 - Q_1)\) i begge retninger.

• Verdier som ligger utenfor disse utstikkerne, kalles uteliggere. Dette er unormalt store eller små verdier. Dette kan si oss noe om vi har mange unormale verdier eller om vi har noen få som vi kanskje kan fjerne ved nærmere statistisk analyse. Vi ser kun én uteligger hos Adelie-pingvinene, med unormalt dypt nebb.

Underveisoppgave

Lag et boksplott over kroppsmasse som funksjon av øya pingvinene er funnet på. Identifiser eventuelle uteliggere.

Underveisoppgave

sns.boxplot(data = pingvindata, x = "island", y = "body_mass_g")

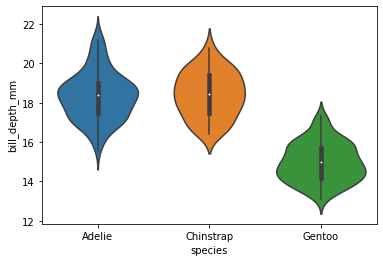
Et alternativ til boksplott er fiolinplott. Prinsippet er ganske likt som med boksplott, men det viser i tillegg fordelingen av de ulike verdiene ved å angi “tynne” og “tykke” områder. Medianen markeres med en hvit prikk, og IQR med en tykk, svart linje. Uteliggere markeres ofte ikke i fiolinplott.

sns.violinplot(data=pingvindata, x='species', y='bill_depth_mm')

<AxesSubplot:xlabel='species', ylabel='bill_depth_mm'>

Varians og standardavvik

I motsetning til IQR, som tar utgangspunkt i medianen, tar varians og standardavvik utgangspunkt i gjennomsnittet. Varians (\(\sigma^2\)) er et mål på variasjonen i et datasett og skrives ofte som \(\sigma^2\). Det er definert som den gjennomsnittlige kvadrerte avstanden til gjennomsnittet av variabelen:

\(\sigma^2 = \frac{1}{n-1}\sum_{i=1}^n(x_i-\bar{x})^2\)

Her er n totalt antall målinger, \(x_i\) er hver måleverdi og \(\bar{x}\) er gjennomsnittet av alle måleverdier. Egentlig bør vi jo dele på \(n\) når vi skal finne gjennomsnittet av denne differansen. Men vi deler på \(n - 1\) istedenfor \(n\) fordi datasettet vårt inneholder et utvalg måledata fra en tenkt fullstendig populasjon. Når vi deler på \(n - 1\) får vi en større varians enn når vi deler på \(n\). En forklaring på dette er at dersom vi hadde samlet inn data fra hele populasjonen, eller gjort tusenvis av målinger av den samme parameteren, ville spredningen (variansen) av målingene vært litt mindre sammenliknet med når vi har færre datapunkter. Vi kaller derfor variansen som er definert ovenfor, for empirisk varians.

Kort oppsummert gjør vi følgende for å regne ut varians:

1. Finner differansen mellom hver måleverdi/hvert datapunkt og trekker fra gjennomsnittet. Dette gir avstanden mellom et målepukt og den gjennomsnittlige verdien.

2. Kvadrerer differansen for å kun få positive verdier. Om vi ikke hadde gjort dette, ville mange negative og positive verdier utlignet hverandre, slik at for eksempel to ekstreme verdier på hver sin side av gjennomsnittet ville gitt 0 i varians.

3. Summerer alle de kvadrerte differansene og deler på antallet målinger (her antallet målinger minus 1). Dette gir den gjennomsnittlige variansen for hele variabelen.

Siden vi kvadrerer avstanden mellom verdier og gjennomsnittet når vi regner ut varians, blir ofte variansen svært stor dersom det finnes noen verdier som ligger et stykke unna gjennomsnittet. I tillegg får den kvadrerte enheter (som \(g^2\) og \(mm^2\), og det er vanskelig å sammenlikne den med måledataene. Derfor er det vanligere å bruke standardavvik som et mål på spredning. Det er definert som den posive kvadratrota av variansen:

\(\sigma = \sqrt{\frac{1}{n-1}\sum_{i=1}^n(x_i-\bar{x})^2}\)

Vi kan enkelt finne variansen og standardavviket med Pandas. Pandas deler på \(n-1\), og ikke \(n\), slik som vi også har gjort.

varians = pingvindata["bill_depth_mm"].var()
standardavvik = pingvindata["bill_depth_mm"].std()

Underveisoppgave

Forklar hva varians og standardavvik er. Lag to Python-funksjoner som regner ut henholdsvis gjennomsnitt og standardavvik. Funksjonene skal gi samme svar som std- og mean-funksjonen i Pandas.

Regresjon

Alle måledata er diskrete verdier. Det betyr at de er ikke-kontinuerlige, altså at det ikke finnes uendelig mange verdier mellom punktene vi har. Vi representerer diskrete data som punkter dersom vi plotter det, mens kontinuerlige data/funksjoner plotter vi som linjer og kurver. Noen ganger kan vi derimot lage kontinuerlige modeller som representerer de diskrete dataene våre. En slik modell kan beskrive både verdier imellom datapunktene, men også utenfor datasettet vi har samlet. En enkel form for modellering er regresjon.

Regresjon

Regresjon er en prosess der vi tilnærmer diskrete data med en kontinuerlig funksjonsmodell.

La oss ta et eksempel der vi har brukt et spektrometer til å måle absorbansen til ulike standardløsninger med permanganationer \(MnO_4^{-}\). Vi har gjort dette fordi vi har en løsning med ukjent innhold av permanganationer. Da trenger vi å gjøre en lineær regresjon for å kunne avgjøre hvilken konsentrasjon absorbansen til den ukjente prøva tilsvarer. Programmet nedenfor lager en standardkurve/kalibreringskurve med funksjonen polyfit fra numpy-biblioteket. Denne funksjonen bruker minste kvadraters metode til å tilpasse funksjonsverdier til datapunktene på en måte som gir minst mulig varians.

import numpy as np
import matplotlib.pyplot as plt

permanganat = [4.0, 8.0, 12.0, 16.0, 20.0] # konsentrasjon i ppm
absorbans = [0.18, 0.32, 0.51, 0.68, 0.85]

reg = np.polyfit(permanganat, absorbans, 1)  # får koeffisientene a og b i en lineær regresjon (grad 1)
x = np.linspace(0, 25, 1000)                 # nye x-verdier for regresjonslinja
y = np.polyval(reg, x)                       # gir et uttrykk på formen y = ax + b, der x = permanganatkonsentrasjonen

plt.scatter(permanganat,absorbans,label='Datapunkter')
plt.plot(x, y, color = 'red',label='Tilpasset kurve')
plt.legend()
plt.title('Standardkurve')
plt.xlabel('$Konsentrasjon av MnO_4^-$ (ppm)')
plt.ylabel('Absorbans')
plt.grid()

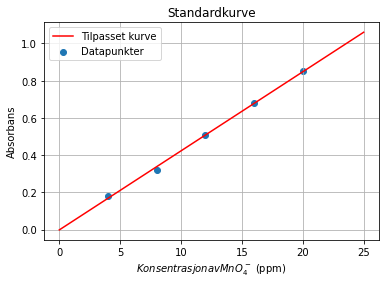
Funksjonen polyfit utfører polynomregresjon på dataene våre, og tar som argument \(x\)- og \(y\)-verdiene i datasettet, og deretter graden av polynomet. Her har vi brukt grad 1 for lineær regresjon. Dette gir en array med koeffisientene a og b for uttrykket \(y = ax + b\). Tilsvarende vil en andregradsregresjon gi koeffisientene a, b og c for \(ax^2 + bx + c\) og så videre. Vi kan dermed bruke disse koeffisientene videre til å lage nye \(y\)-verdier basert på de opprinnelige \(x\)-verdiene. Til det kan vi bruke funksjonen polyval, som tar to parametre: koeffisientene som er gitt av polyfit-funksjonen og de nye x-verdiene som vi skal regne ut funksjonsverdier til.

La oss si at den ukjente prøva med permanganationer ga en absorbans på 0.40. Vi kan bruke regresjonskurven vår til å finne hva slags konsentrasjon dette tilsvarer på følgende måte:

import numpy as np
import matplotlib.pyplot as plt

permanganat = [4.0, 8.0, 12.0, 16.0, 20.0] # konsentrasjon i ppm
absorbans = [0.18, 0.32, 0.51, 0.68, 0.85]
ukjent_abs = 0.40

# Gjør regresjonen
reg = np.polyfit(permanganat, absorbans, 1)  # får koeffisientene a og b i en lineær regresjon (grad 1)
x = np.linspace(0, 25, 1000)                 # nye x-verdier for regresjonslinja
y = np.polyval(reg, x)                       # gir et uttrykk på formen y = ax + b, der x = permanganatkonsentrasjonen

# Regner ut den ukjente konsentrasjonen
ukjent_kons = (ukjent_abs - reg[1])/reg[0]
print("Konsentrasjonen til permanganat =", round(ukjent_kons,1), "ppm.")

plt.scatter(permanganat,absorbans,label='Datapunkter')
plt.plot(x, y, color = 'red',label='Tilpasset kurve')
plt.plot(ukjent_kons, ukjent_abs, linestyle = " ", marker = "o", color = 'seagreen', label = "Ukjent løsning")
plt.legend()
plt.title('Standardkurve')
plt.xlabel('$Konsentrasjon av MnO_4^-$ (ppm)')
plt.ylabel('Absorbans')
plt.grid()

Konsentrasjonen til permanganat = 9.5 ppm.

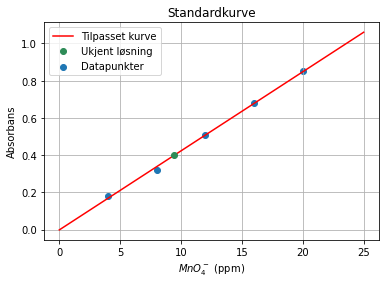
Underveisoppgave

Fritt klor (\(Cl_2\)) finnes i en del drikkevann fordi klorforbindelser blir tilsatt klorforbindelser for å desinfisere vannet. I programmet nedenfor har vi lagt inn en serie målinger som er gjort på standardløsninger av konsentrasjonen av fritt klor i vann gitt i ppm. Gjør en regresjon av dataene og lag en standardkurve. Regn ut konsentrasjonen av fritt klor i en drikkevannsprøve med absorbans 0.656 ppm.

Løsningsforslag

import numpy as np
import matplotlib.pyplot as plt

klor = [0, 0.50, 1.00, 1.50, 2.00] # konsentrasjon i ppm
absorbans = [0.000, 0.270, 0.543, 0.813, 1.084]
ukjent_abs = 0.656

# Gjør regresjonen
reg = np.polyfit(klor, absorbans, 1)  # får koeffisientene a og b i en lineær regresjon (grad 1)
x = np.linspace(0, 2.2, 1000)                 # nye x-verdier for regresjonslinja
y = np.polyval(reg, x)                       # gir et uttrykk på formen y = ax + b, der x = permanganatkonsentrasjonen

# Regner ut den ukjente konsentrasjonen
ukjent_kons = (ukjent_abs - reg[1])/reg[0]
print("Konsentrasjonen til fritt klor =", round(ukjent_kons,2), "ppm.")

plt.scatter(klor,absorbans,label='Datapunkter')
plt.plot(x, y, color = 'red',label='Tilpasset kurve')
plt.plot(ukjent_kons, ukjent_abs, linestyle = " ", marker = "o", color = 'seagreen', label = "Ukjent løsning")
plt.legend()
plt.title('Standardkurve')
plt.xlabel('Konsentrasjon av Cl$_2$ (ppm)')
plt.ylabel('Absorbans')
plt.grid()
plt.show()

Når vi har utført regresjon, kan vi også forutsi datapunkter som er utenfor datapunktene våre. Dette kaller vi ekstrapolering. Ved å ekstrapolere kan vi forutsi hvordan et system har vært eller kommer til å bli. En skal derimot være svært forsiktig med å trekke slutninger basert på ekstrapolering! Det kan likevel være en god indikasjon på trender og utviklingen i et system.

Vi kan også lage visualiseringer med automatiske regresjonskurver. La oss vende tilbake til pingvinene våre. For å se om det kan være noen sammenhenger som er verdt å lage en modell av, kan vi enkelt visualisere mange ulike variabler mot hverandre ved å bruke et parplott (pairplot) fra seaborn-biblioteket:

import seaborn as sns

sns.pairplot(data = pingvindata, hue = "species")

<seaborn.axisgrid.PairGrid at 0x28083e73220>

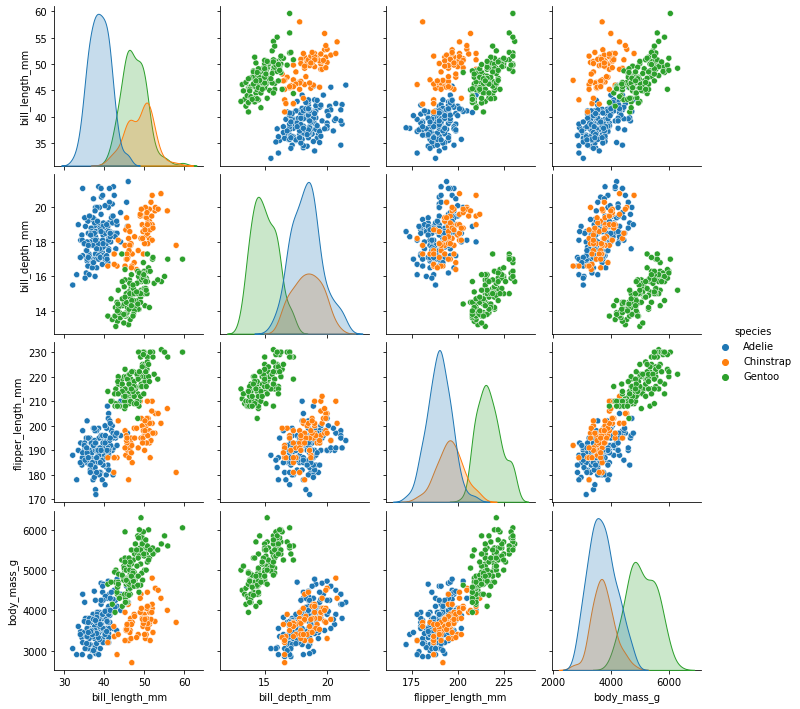
Vi tar utgangspunkt i kroppsmasse og vingelengde, som ser ut til å være lineært avhengig av hverandre. Et plott med regresjonslinje kan vi lage ved å bruke funksjonen lmplot (eller regplot) fra seaborn-biblioteket:

sns.lmplot(data = pingvindata, x = "body_mass_g", y = "flipper_length_mm")

<seaborn.axisgrid.FacetGrid at 0x280879f8430>

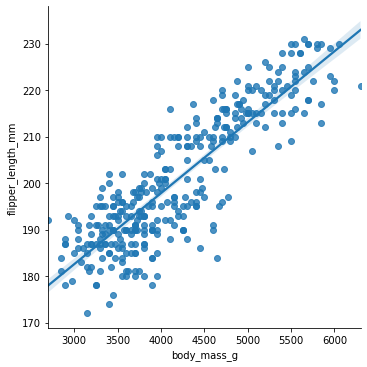
Vi ser at vi får en regresjonslinje med et svakt blått område på hver side av linja. Dette området indikerer usikkerheten i verdiene. Desto større dette området er, desto mer usikkert er det at regresjonslinja er en god modell i dette området. Vi kan gjøre dette tydeligere ved å velge to variabler som ikke varierer så godt lineært:

sns.lmplot(data = pingvindata, x = "bill_depth_mm", y = "flipper_length_mm")

<seaborn.axisgrid.FacetGrid at 0x28087a06e20>

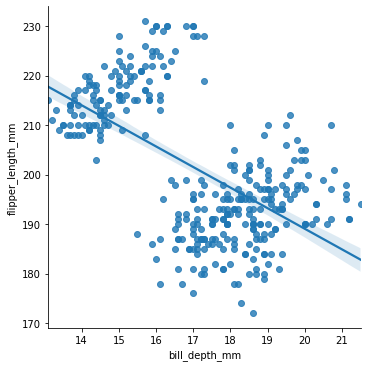
Vi kan også gjøre regresjon på ulike variabler, slik som ulike arter, for seg:

sns.lmplot(data = pingvindata, x = "bill_depth_mm", y = "flipper_length_mm", hue = "species")

<seaborn.axisgrid.FacetGrid at 0x280864bb970>

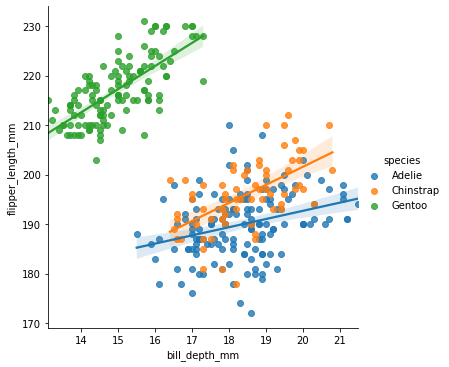
Korrelasjon

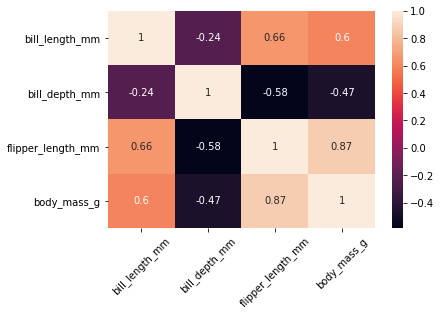
Korrelasjoner kan brukes til å analysere sammenhenger mellom parametre. Korrelasjon beregnes som en verdi mellom -1 og 1. En verdi som brukes ofte som mål på korrelasjon, er Pearsons korrelasjonskoeffisient. Positiv korrelasjon betyr at det er en proporsjonal sammenheng mellom parametrene, og en negativ korrelasjon betyr at det er en omvendt proporsjonal sammenheng. Desto større absoluttverdien til korrelasjonen er, desto større sammenheng er det mellom parametrene. Vi kan visualisere korrelasjon gjennom et korrelasjonsplott:

corr = pingvindata.corr()     # Regner ut korrelasjonskoeffisientene
sns.heatmap(corr, annot=True) # Lager visualisering. Parameteren annot = True gir tallene i boksene.
plt.xticks(rotation=45)       # Roterer x-akseteksten 45 grader
plt.show()

iris.corr()

	sepal_length	sepal_width	petal_length	petal_width
sepal_length	1.000000	-0.117570	0.871754	0.817941
sepal_width	-0.117570	1.000000	-0.428440	-0.366126
petal_length	0.871754	-0.428440	1.000000	0.962865
petal_width	0.817941	-0.366126	0.962865	1.000000

pingvindata.corr()

	bill_length_mm	bill_depth_mm	flipper_length_mm	body_mass_g
bill_length_mm	1.000000	-0.235053	0.656181	0.595110
bill_depth_mm	-0.235053	1.000000	-0.583851	-0.471916
flipper_length_mm	0.656181	-0.583851	1.000000	0.871202
body_mass_g	0.595110	-0.471916	0.871202	1.000000

Vi ser for eksempel at det er ganske stor positiv korrelasjon mellom nebblengde og lengden på vingene (luffene). Det betyr at dersom en pingvin har langt nebb, har den ofte også lange vinger. Det er derimot negativ korrelasjon mellom nebbdybde og vingelengde, som betyr at desto dypere nebb, desto kortere vinger har pingvinen.

Det er derimot viktig å ikke blande korrelasjon med årsak-virkning (kausalitet). Den ene tingen forklarer ikke nødvendigvis den andre (selv om det kan gjøre det), det er bare en sammenheng mellom parametrene.

Underveisoppgave

I programmet nedenfor finner du datasettet “iris.txt”. Les inn datasettet og gjør en korrelasjonsanalyse av variablene. Hvilke faktorerer korrelerer positivt og negativt med hverandre? Finnes det logiske forklaringer på det?

Løsningsforslag

import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns

iris = pd.read_csv("iris.txt")
corr = iris.corr()

sns.heatmap(corr, annot=True,)
plt.xticks(rotation=45)  
plt.show()

Videoer

I videoen nedenfor kan du få en innføring eller repetisjon i den grunnleggende teorien bak regresjonsanalyse:

Oppgaver

Oppgave 1

Modifiser programmet nedenfor slik at det i tillegg til gjennomsnittet også regner og skriver ut det gjennomsnittlige avviket. Avviket for en måling er hvor langt unna gjennomsnittet det er. Det gjennomsnittlige avviket er da gjennomsnittet av alle avvikene.

Oppgave 2

Som du oppdaget i forrige oppgave er ikke gjennomsnittlig avvik et veldig godt spredningsmål (forstår du hvorfor?). Legg til i koden (uten å slette det du gjorde i oppgave 1) at den også regner ut det gjennomsnittlige kvadratavviket. Kvadratavviket for en måling er avstanden til gjennomsnittet opphøyd i 2, og igjen skal vi finne snittet av alle disse. Er gjennomsnittlig kvadratavvik et bedre spredningsmål enn det du fant i oppgave 1? Hvorfor/hvorfor ikke?

Oppgave 3

Det vi fant i oppgave 2 har et kortere navn enn gjennomsnittlig kvadratavvik. Hva heter det? Hva må endres når dataene våre er målinger fra en større populasjon, slik tilfellet er her? Gjør denne endringen, og finn også til slutt standardavviket. Skriv ut også dette.

Oppgave 4

1. Les fila temperatur.csv.

2. Beregn gjennomsnitt og standardavvik for temperaturen i datasettet ved å bruke innebygde Pandas-funksjoner.

3. Beregn medianen for temperaturen, og deretter første og andre kvartil. Hva sier disse målingene deg om datasettet?

4. Beregn interkvartilbredden og sammenlikn med standardavviket. Hva er forskjeller og sammenhenger mellom disse målene?

Oppgave 5

Lag et histogram som viser fordelingen av temperatur i datafila temperatur.csv.

Oppgave 6

1. Gjør en regresjon av følgende data der vi har målt strekning i meter og tid i sekunder under en gåtur:

tid = [1, 2, 3, 4, 5]
strekning = [2.1, 3.9, 5.5, 8.4, 10.2]

2. Begrunn valget av modell.

3. Bruk modellen til å forutsi hvor mange meter vi vil ha gått etter 2 timer hvis vi følger denne modellen. Hva forutsetter dette?

Oppgave 7

Bruk datasettet i Trinket-vinduet nedenfor og finn enklest mulig (med én kodelinje) både gjennomsnitt og standardavvik for mål scoret av hjemmelag og bortelag i Eliteserien 2023.

Oppgave 8 (utfordring)

Koden i Trinket-vinduet gir oss et plott over hvilke lag som scoret flest mål på hjemmebane i 2023-sesongen. Utvid koden til å også vise oss

• hvilke lag som scoret flest mål på bortebane

• hvilke lag som slapp inn flest mål på hjemmebane

• hvilke lag som slapp inn flest mål på bortebane

Oppgave 9 (utfordring)

Lag et plott som hvilke resultater som var mest typiske i 2023-sesongen. Dette gjør du med funksjonen sns.kdeplot, som oppfører seg ganske likt sns.catplot, som vist ovenfor. Du må fylle inn følgende argumenter til funksjonen:

• data: hvilket datasett du bruker

• x: hva som skal plottes på x-aksen (for eksempel mål til bortelaget)

• y: hva som skal plottes på y-aksen (for eksempel mål til hjemmelaget)

• fill="true" (for at plottet skal være lettere å tolke)

(Du trenger ikke kind="violin" til dette plottet.)

Oppgave 10 (utfordring)

Som vist i Trinket-vinduet over, kan vi i stedet for å se på alle kampene lage et plott som viser de mest typiske resultatene for en delmengde av resultatene. I eksempelet kan vi se bare på Bodø/Glimt sine hjemmekamper (glimt_hjemme) i stedet for hele datasettet (fotballdata). Lag et plott over denne delmengen (som du gjorde i oppgave 6), og finn ut hvilke(t) resultat(er) som er mest typiske når Bodø/Glimt spiller hjemme. Gjør det samme for Bodø/Glimt borte og Tromsø (hjemme og borte).