Symbolsk utregning (CAS)#
Bruk av CAS (Computer Algebra System) i Python#
Her er en liten oversikt over hva du kan gjøre i CAS-verktøyet i Python.
from sympy import * # CAS-verktøyet i Python heter Sympy
# Vi definerer de bokstavene som skal brukes som symboler i likninger, funksjoner og uttrykk
x = symbols("x")
Faktorisering#
x, y = symbols("x y") # Vi kan definerer flere symboler på samme linje, eller hver for seg
factor(x + 2*y*x)
\[\displaystyle x \left(2 y + 1\right)\]
Løse likninger#
solve(x**2 - 4, x)
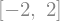
Derivere#
diff(uttrykk, x)

Integrere#
integrate(4*x**3, x) # Ubestemt integrasjon
\[\displaystyle x^{4}\]
integrate(cos(x**2), (x, -oo, oo)) # Bestemt integrasjon med grenser (uendelig lages med to av bokstaven o)
\[\displaystyle \frac{\sqrt{2} \sqrt{\pi}}{2}\]
Grenseverdier#
limit(sin(x)/x, x, 0)
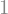
Differensiallikninger#
Vi løser difflikninga \(y′′−y=e^t\):
y = Function('y')
difflikning = Eq(y(t).diff(t, t) - y(t), exp(t))
dsolve(difflikning, y(t))
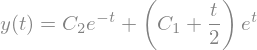
y = Function('y')
difflikning2 = Eq(y(t).diff(t), y(t))
dsolve(difflikning2, y(t))

