Grunnleggende programmering (oppgaver)#
Her er litt teori og oppgaver som kan hjelpe deg å komme i gang med det viktigste innen realfaglig programmering. Bruk gjerne de innebygde kodeboksene til å lage og kjøre programmer underveis.
1. Variabler#
Variabel
En programmeringsvariabel er en størrelse som lagrer en verdi i et program.
Her er et eksempel med variablene m og v. Hva bruker vi de til i programmet nedenfor?
m = 1 # Masse
v = 2 # Hastighet
kinetisk_energi = 0.5*m*v**2
print("Den kinetiske energien er:", kinetisk_energi, "J.")
Den kinetiske energien er: 2.0 J.
Vi kan også bruke matematiske funksjoner som kvadratrot og trigonometriske funksjoner. Da må vi importere et bibliotek som inneholder disse funksjonene. Det enkleste er å importere alt fra biblioteket pylab. Det gjør vi slik:
from pylab import *
kvadratrot = sqrt(4)
sinus = sin(radians(30))
print("Kvadratrota av 4 er:", kvadratrot, "Sinus til 30 grader er:", sinus)
Kvadratrota av 4 er: 2.0 Sinus til 30 grader er: 0.49999999999999994
Merk at vi måtte gjøre om vinkelmålet til radianer (som er et vinkelmål man lærer om i R-matte) til grader. Det samme prinsippet gjelder for øvrig i GeoGebra.
Oppgave 1.1
Bruk kodeboksen nedenfor til å lage relevante variabler slik at programmet regner ut arealet av en trekant med grunnlinje 4 og høyde 2. Programmet inneholder litt kode fra før til å hjelpe deg på vei.
Løsningsforslag
g = 4
h = 2
A = g*h/2
print("Arealet til trekanten er:", A)
Oppgave 1.2
Lag et program som regner ut radius til en sirkel med arealet 4.
Løsningsforslag
A = 4
pi = 3.1415 # Vi skal se hvordan vi kan bruke en forhåndsdefinert pi seinere
r = (A/pi)**0.5 # Vi skal se på hvordan vi kan ta rota uten å opphøye i 0.5 seinere
print("Radius til sirkelen er:", r)
Ekstra: Oppgave 1.3
For å ta input fra brukeren av programmet istedenfor å skrive variabelverdier rett inn i programmet, kan vi bruke input-funksjonen til Python.
tall = float(input(“Skriv et tall: “))
Lag et program som bruker en formel fra matematikken til å regne ut noe. Bruk input-funksjonen til å hente variabelverdier fra brukeren. Hvis du lurer på hva “float”-kommandoen foran input gjør, kan du lese mer om det i 1.1 nedenfor.
1.1 Variabeltyper#
I matematikk har vi ulike tallmengder, som reelle tall, irrasjonale tall, rasjonale tall, naturlige tall, hele tall og komplekse tall. Disse tallmengdene er uendelig store, som betyr at de ikke kan eksistere på en datamaskin. Vi har derfor en del andre tallmengder og variabeltyper. For eksempel heter desimaltall float fordi ikke alle desimaltall er representert på en datamaskin. Det er altså en annen tallmengde. De viktigste variabeltypene ser du her:
Datatype |
Forklaring |
Eksempel |
|---|---|---|
Heltall (int) |
Hele tall |
42 |
Flyttall (float) |
Desimaltall |
3.1415 |
Streng (str) |
Tekst |
“Hei!” |
Boolsk |
Sannhet |
True eller False |
Når vi ønsker input fra en bruker av et program, må vi spesifisere hvilken variabeltype vi ønsker at inputen skal bli tolket som. Standard er tekst, men hvis vi for eksempel “adderer” teksten “4” med “2”, får vi “42”, mens tallet 4 + tallet 2 gir tallet 6. Eksempelet nedenfor illustrerer dette.
tekst1 = input("Skriv et tall: ")
tekst2 = input("Skriv et tall til: ")
tall1 = float(tekst1)
tall2 = float(tekst2)
tullsvar = tekst1 + tekst2
tallsvar = tall1 + tall2
print("Summen av teksten er:", tullsvar, "og summen av tallene er:", tallsvar)
Skriv et tall: 4
Skriv et tall til: 2
Summen av teksten er: 42 og summen av tallene er: 6.0
Input er ikke nødvendig for annet enn å lage et mer interaktivt program. Men hvis du lager et program med input, bør du legge til input helt til slutt. Start med å gi variablene verdier, og test at programmet fungerer. Deretter kan du bruke input på de variablene du ønsker. Dette er for å unngå å måtte taste inn input-verdier hver gang du kjører programmet ditt, spesielt hvis det inneholder feil du må rette opp!
2. Vilkår (if-tester)#
Vilkår (if-test)
Et vilkår, eller en betingelse, er en logisk test for å sjekke om et kriterium er oppfylt. Dersom kriteriet er oppfylt, utføres det en handling. Dersom kriteriet ikke er oppfylt, blir ikke handlingen utført.
tall = 42
if tall < 5:
print("Tallet er veldig lite.")
elif tall < 20:
print("Tallet er ganske lite.")
elif tall < 50:
print("Tallet er passe stort.")
elif tall < 100:
print("Tallet er ganske stort.")
else:
print("Tallet er enormt!")
Tallet er passe stort.
Det er noen ting å huske på her:
Alt som er rykket inn utføres kun hvis if-testen ovenfor er sann. Innrykk er derfor viktig for strukturen.
“elif” står for “else if”, og sjekker noe nytt, mens “else” brukes for å gjøre noe dersom ingen av kriteriene under “if” og “elif” er sanne.
Det er den første if-testen som er sann i en serie av if-elif-else som utføres. Alle andre overses. Dersom vi skriver “if” en gang til, begynner vi på en ny serie med if-elif-else.
Vi må begynne med “if”, mens “elif” og “else” er valgfritt.
De logiske operatorene vi kan velge mellom, er:
Symbol |
Betydning |
|---|---|
> |
større enn |
< |
mindre enn |
== |
lik |
!= |
ikke lik |
<= |
mindre enn eller lik |
>= |
større enn eller lik |
Oppgave 2.1
Lag et program der du sjekker om et tall er positivt, negativt eller null, og skriver ut relevante setninger. Du kan ta utgangspunkt i programkoden i kodeboksen her:
Oppgave 2.2
Lag et program med en variabel kalt pH. Programmet skal skrive ut om løsningen med denne pH-en er sur, basisk eller nøytral.
Oppgave 2.4
I et programmeringspuslespill skal du bruke ferdige kodeblokker til å pusle sammen et program. Løs dette programmeringspuslespillet. Programmet skal skrive ut antallet løsninger i en andregradslikning. Når du er ferdig, kan du prøve dette puslespillet, som er en litt mer avansert variant. Forklar forskjellen på programmene.
3. Løkker#
Den kanskje viktigste strukturen i programmering er løkker. De lar datamaskinen gjenta en operasjon så mange ganger vi vil. Det er dette som er datamaskinens styrke.
Løkker
En løkke er en struktur som gjør at vi kan gjenta kode. Ofte skiller vi mellom en telleløkke, som gjentar noe et visst antall ganger, og en tilstandsløkke, som gjentar så lenge noe er sant. I Python heter disse henholdsvis for-løkke og while-løkke.
partall = 0
for i in range(5): # Gjenta 5 ganger (i går igjennom intervallet [0, 1, 2, 3, 4])
partall = partall + 2
print(partall)
2
4
6
8
10
partall = 0
while partall < 10: # Gjenta så lenge partall er mindre enn 10
partall = partall + 2 # Øk partallsvariabelen med 2
print(partall)
2
4
6
8
10
Studer løkkene og prøv å forstå hvordan de virker. Legg merke til at alt som er rykket inn til høyre, tilhører løkka og gjentas hver gang løkka kjører.
Det er viktig å forstå hvordan løkkene fungerer. For å illustrere dette, kan vi sette opp en løkketabell som viser verdien til de ulike variablene i ei løkke. La oss bruke følgende program som utgangspunkt:
a = 0
for i in range(5):
a = a + 1
b = a*i
En løkketabell som beskriver hva verdien til alle variabelene er før og underveis i løkka, er gitt nedenfor. Bruk løkka og tabellen og prøv å forstå hva som skjer!
Løkkerunde |
i |
a |
b |
|---|---|---|---|
Startverdi |
- |
0 |
- |
1 |
0 |
1 |
0 |
2 |
1 |
2 |
2 |
3 |
2 |
3 |
6 |
4 |
3 |
4 |
12 |
5 |
4 |
5 |
20 |
Vi kan printe ut variablene underveis i løkka og se at vi faktisk får det samme (husk at kategorien “løkkerunde” ikke er en variabel):
a = 0
print("i | a | b") # Printer kun én gang
for i in range(5):
a = a + 1
b = a*i
print(i,"|", a,"|", b) # Printer hver gang i løkka
i | a | b
0 | 1 | 0
1 | 2 | 2
2 | 3 | 6
3 | 4 | 12
4 | 5 | 20
Oppgave 3.1
Lag et program som skriver ut “Du er flink til å programmere!” tusen ganger. Hvilken funksjon har “tellevariabelen” (i) her?
Oppgave 3.2
Programmet nedenfor skal finne summen av de 100 første tallene i en tallfølge der hvert ledd er den dobbelte av det forrige. Forklar hvordan programmet fungerer. Endre gjerne på ulike variabler og test hva utfallet blir for å forstå hvordan programmet fungerer.
Oppgave 3.3
Skriv om programmet ovenfor slik at du benytter en while-løkke istedenfor en for-løkke.
Oppgave 3.4
Skriv om programmet ovenfor slik at du benytter en while-løkke istedenfor en for-løkke.
Oppgave 3.5
Lag en løkketabell av programmet nedenfor:
a = 0
for i in range(5):
b = a*i
a = a + 1
Oppgave 3.6
Hva skrives ut i følgende program? Prøv å undersøke dette for hånd. Til slutt kan du sjekke ved å kopiere programmet inn i en editor og kjøre det.
a = 0
for i in range(5):
b = a*i
print(b)
a = a + 1
print(a)
Oppgave 3.7
Programmene nedenfor skal regne ut hvor lang tid det tar før du har doblet beløpet ditt i banken gitt en årlig rente på 5 % og en startkapital på 5000 kroner, men programmet fungerer ikke som det skal. Hva er feil? Rett opp programmet slik at det fungerer.
3.1 Løkker og lister#
Lister er en datastruktur i Python som lar oss spare på ulike verdier i samme variabel. Eksempel på hvordan lister kan brukes, er slik:
tom_liste = [] # Lager en tom liste
tall = [1, 2, 3.5] # Liste med tre tall
dyr = ["Stumpneseape", "Lemur", "Sjøku"] # Liste med tre dyr (tekststrenger)
tom_liste.append(24)
print("Append-funksjonen legger til elementer i lista. Vi får:", tom_liste)
Lister er en god kombinasjon med løkker, siden løkker kan generere ulike tallverdier som vi kan spare på i listene. For eksempel slik:
startkapital = 5000
penger = startkapital
år = 0
rente = 0.01
år_liste = [0]
penger_liste = [startkapital]
while penger < startkapital*2:
penger = penger + penger*rente
år = år + 1
år_liste.append(år)
penger_liste.append(penger)
Oppgave 3.8
Forklar hvordan programmet ovenfor fungerer.
Siden vi nå har en variabel som inneholder pengene ved et hvert år, er det en gyllen mulighet til å visualisere hvordan pengeutviklingen er. Da må vi først se litt på hvordan vi kan plotte.
4. Plotting#
Vi kan enkelt plotte lister med data på denne måten:
from pylab import * # Importerer relevante plotteverktøy
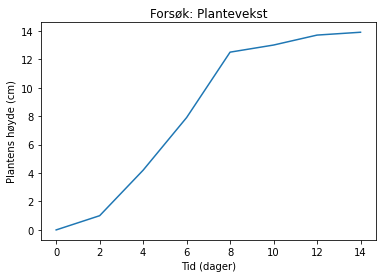
tid = [0, 2, 4, 6, 8, 10, 12, 14] # dager
plantehøyde = [0, 1, 4.2, 7.9, 12.5, 13, 13.7, 13.9] # cm
plot(tid, plantehøyde)
title("Forsøk: Plantevekst")
xlabel("Tid (dager)")
ylabel("Plantens høyde (cm)")
show()
Det finnes utrolig mange måter å modifisere et plott på. Programmet nedenfor plotter miljøgifter i ulike organismer i to innsjøer. Studer programmet og eksperimenter med ulike verdier. Du kan finne verdier for farger, linjestiler, markører og liknende ved å google «python plotting colors» og tilsvarende. Biblioteket som inneholder plotting, heter matplotlib, noe du kan se av søkeresultatene dine. Du må bruke internett flittig når du lurer på noe i programmering!
Vi kan også plotte funksjoner. Da må vi spesifisere hvilke verdier av x vi ønsker å plotte for. Disse x-verdiene kan vi generere enkelt ved å bruke en kommando som heter linspace(a, b, n). Denne genererer et intervall fra a til b med n punkter. Test programmet nedenfor og prøv for eksempel med n = 4 (altså at antall x-verdier er 4). Hva skjer da, og hvorfor?
Oppgave 4.1
Prøv å plotte verdiene fra renteprogrammet nedenfor. Eksperimenter med ulike verdier av startkapital og rente, og se hvordan utviklingen endrer seg.
*5. Funksjoner#
Funksjoner er å regne som en grunnstruktur i programmering, men det er ikke en nødvendig grunnstruktur for å lage enkel kode for å utforske matematikk og naturfag. Til tross for dette er funksjoner nyttig å kunne, men husk at det er mer en kodeteknisk ferdighet enn en ferdighet vi kan bruke for å forstå realfag.
Det er viktig å vite at funksjoner i programmering ikke er det samme som funksjoner i matematikk. De KAN ha samme virkemåte, men trenger ikke det. La oss representere den matematiske funskjonen \(f(x) = 2x^2 - x + 1\) som en Python-funksjon:
def f(x):
return 2*x**2 - x + 1
Vi definerer en funksjon med kodeordet def og gir den et funksjonsnavn, her f. Deretter spesifiserer hva inn-verdien/variabelen til funksjonen skal hete. Her kaller vi den x. I programmering kaller vi en slik størrelse for en parameter. Gitt én verdi av x, skal funksjonen returnere (spesifisert ved return-kommandoen) en funksjonsverdi.
Her har vi bare definert funksjonen. Vi har ikke brukt den enda, så vi får ikke noe output her. La oss bruke funksjonen:
print(f(1))
2
Som vi ser, får vi funksjonsverdien til f(1). Nå har vi brukt funksjonen vi tidligere har definert. Dette heter å “kalle på” funksjonen.
Poenget med funksjoner er i hovedsak to ting:
Kodestrukturering.
Gjenbruk av kode.
Det er spesielt sistnevnte poeng som er sentralt. Ved å definere en funksjon kan vi bruke denne funksjonen flere ganger i programmet vårt, for eksempel slik:
def f(x):
return x + 1
addisjon = f(1) + f(3)
subtraksjon = f(1) - f(3)
print(addisjon, subtraksjon)
for x in range(5):
print(f(x))
6 -2
1
2
3
4
5
Oppgave 5.1
Forklar hvordan programmet ovenfor fungerer.
Oppgave 5.2
I programmet nedenfor definerer vi en funksjon som regner ut volumet til en sylinder. Lag en annen funksjon i samme program som regner ut volumet til ei kule.
(\(V_{kule} = \frac{4}{3}\pi r^3\))
